Natural Resources as Stock Market Trouble Alarm
- H-Barrio

- Jul 27, 2021
- 4 min read
Stock markets shocks are notoriously difficult to predict. In general, periods of high volatility can lead to both large market gains and losses, making volatility a not very reliable indicator to predict a crash. The most recent large crash, the COVID19 downturn, was not adequately predicted by many of the large players in financial markets—the few who did walked out with very, very large profits. Traditionally, natural resources have been used to predict larger market moves, for example, using copper prices or "Dr. Copper" to predict industrial returns. Copper is also unreliable, as described in this Nikkei article. Is there a sufficiently reliable base materials price indicator that can lead the prices higher up on the manufacturing chain?
The best candidate we could find for this task is the IGE ETF. This ETF attempts to "track the investment results of an index composed of North American equities in the natural resources sector." We will hypothesize that North American companies in the natural resources sector are devoting resources themselves to predict future market conditions, and movements on their pricing can predict future movements on the market overall. Thus, shocks in the base of the pyramid will result in shocks higher up the supply and transformation chain, being the natural resources producers the first to predict a shock, or at least being the companies with the highest interest in predicting these events.
We will test our hypothesis using the Quantconnect backtesting tool. The algorithm will be at the end of the post, after our contact information. We will start defining our import needs and the basics of the algorithm:
import numpy as np
import pandas as pd
class NaturalResources(QCAlgorithm):
def Initialize(self):
self.SetStartDate(2016, 7, 1)
self.SetCash(1000000)
self.SetBrokerageModel(BrokerageName.AlphaStreams)
rebalance_period = timedelta(days = 7)
self.SetPortfolioConstruction(
InsightWeightingPortfolioConstructionModel(
rebalance_period
))
self.Settings.RebalancePortfolioOnInsightChanges = False
self.SetExecution(ImmediateExecutionModel())
res = Resolution.Hour
self.UniverseSettings.Resolution = res
market = ['SPY']
bonds = ['TLT']
signals = ['IGE']
self.market = [self.AddEquity(ticker, res).Symbol for ticker in
market]
self.bonds = [self.AddEquity(ticker, res).Symbol for ticker in
bonds]
self.signals = [self.AddEquity(ticker, res).Symbol for ticker in
signals]
self.AddAlpha(NaturalResourcesEvent(self.market,
self.bonds,
self.signals,
))We need NumPy for extreme probability calculations and pandas for handling the history calls. Then we initialize our Natural Resources algorithm with an hourly resolution and declaring SPY as our main investment vehicle, TLT as our safe haven during periods of predicted stock market shock, and IGE as our predictive signal.
Next, we have to initialize our signal generating alpha module:
class NaturalResourcesEvent(AlphaModel):
""" """
def __init__(self,
market,
bonds,
signals):
self.Name = 'Natural Resources Event'
self.market = market
self.bonds = bonds
self.signals = signals
# Rolling mean of signal:
self.rolling_mean = 55
self.past_days = 365
# Out of market waiting days:
self.wait_days = 15
# Percentiles of extreme:
self.extreme_p = 5
self.be_in = True
self.hold_days = timedelta(days=1)
self.gain = 0.02
self.dcount = FalseWe will use the mean 55-day rolling price for the past 365 days for our extreme event prediction. We will weather the shock for 15 days, and the shock is defined by an extreme 5 percentile movement. Then at every data slice, we will generate the required insights:
def Update(self, algorithm, data):
if algorithm.Time.hour != 10 or algorithm.Time.minute !=0:
return []
insights = []
# Sample to detect extreme observations:
hist = algorithm.History(self.signals, self.past_days,
Resolution.Daily)['close']
hist = hist.unstack(level=0).dropna()
# Rolling mean smoothing out of values:
hist_shift = hist.rolling(window=self.rolling_mean).mean().dropna()
# As returns:
returns_sample = (hist / hist_shift - True)
# Extreme observations at given percentile
pctl_b = np.nanpercentile(returns_sample,
self.extreme_p,
axis=int(False))
extreme_b = returns_sample.iloc[-True] < pctl_b
alarms_on = extreme_b[self.signals].any()
# Determine whether 'in' or 'out' of the market
if alarms_on:
self.be_in = False
if self.dcount >= self.wait_days: self.be_in = True
if self.be_in:
for symbol in self.market :
weight = int(True)
insights.append(Insight(symbol, self.hold_days,
InsightType.Price,
InsightDirection.Up,
self.gain, int(True),
self.Name, weight))
self.dcount = False
return insights
else:
algorithm.Log('Market Event incoming. Entering safe
positions.')
for symbol in self.bonds:
insights.append(Insight(symbol, self.hold_days,
InsightType.Price,
InsightDirection.Up,
self.gain, int(True),
self.Name, int(True)))
self.dcount += True
return insightsWe act only at 10:00 AM; we check the history of the price for IGE and obtain a sample of the returns; if the last value of returns is below our percentile limit, we will call it a natural resources alarm. While the alarm is on, we will avoid the stock market for 15 days and place our assets into bonds.
For the past 5 years, this has been the performance:
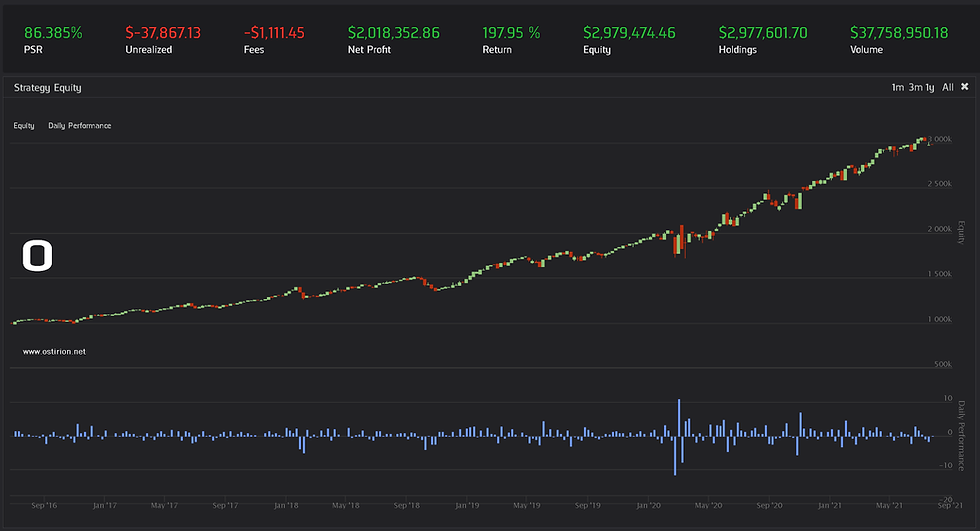
Not a bad performance, IGE seems to pick, sooner or later, most of the bad market conditions that appeared in 2017, 2018, and 2020. The model offers a backtest Sharpe Ratio of 1.68 with a beta of 0.32, remarkable for a SPY/TLT based model. Of course, the fleeing to bonds must be maintained for the model to properly work in the future, although an alternative is to go to cash in the presence of a possible future shock. This test is anecdotal evidence so far, so let us try for a longer period since the inception of the IGE ETF to see how it behaves. We will change the start date to:
self.SetStartDate(2001, 11, 1)The results are these:

Not bad, not remarkable. The natural resources fail to advance two critical points, the 2008 subprime crisis, and the 2010 flash crash. Still, for these 20 years, the Sharpe Ratio is 0.86 with a beta of 0.5, a 12% annual return at acceptable risk levels.
There are possibly other signal and instrument combinations that may lead to similar results. The information has to be there. The market has to behave as a production measurement device in the absence of financial manipulation. At least it should behave as such, and certain buried pieces of information should maintain pricing power for the market as a whole. The question for beating the market now is finding those signals, signals that endure in time and are relatively difficult to detect. We will discuss further signals and instrument pairs in upcoming posts. The model, in its final form, is at the end of the post after the disclaimer and invitation to connect.
Information in ostirion.net does not constitute financial advice; we do not hold positions in any of the companies or assets that we mention in our posts at the time of posting. If you require quantitative model development, deployment, verification, or validation, do not hesitate and contact us. We will also be glad to help you with your machine learning or artificial intelligence challenges when applied to asset management, trading, or risk evaluations.


Comments